Unidad 3

LIMITES Y CONTINUIDAD

3.1 Limite de una sucesión

3.2 Limite de una función de variable real 

3.3 Cálculo de limites 

3.4 Propiedades de los limites

3.5 Limites laterales

3.6 Limites infinitos y limites al infinito

3.7 Asintotas

3.8 Funciones continuas y discontinuas en un punto y en un intervalo

3.9 Tipos de discontinuidades

3.1 Limite de una sucesión

El límite de una sucesión es uno de los conceptos más antiguos del análisis matemático. El mismo da una definición rigurosa a la idea de una sucesión que se va aproximando hacia un punto llamado límite. Si una sucesión tiene límite, se dice que es una sucesión convergente, y que la sucesión converge o tiende al límite. En caso contrario, la sucesión es divergente.

La definición significa que eventualmente todos los elementos de la sucesión se aproximan tanto como queramos al valor límite. La condición que impone que los elementos se encuentren arbitrariamente cercanos a los elementos subsiguientes no implica, en general, que la sucesión tenga un límite.

El límite de una sucesión particular es generalmente un número o un punto definido L, con la condición que todos los términos de esa sucesión particular estén muy cerca de L para grandes cifras de n. En caso de que el límite esté presente, se dice entonces que la sucesión es convergente y converge en el punto definido L. En el caso complementario, se dice que la sucesión es divergente. Matemáticamente la definición puede ser demostrada suponiendo an} sea la sucesión y l un número real. Si por cada ε › 0 entonces encontramos m N, tal que, n N, es l y se escribe an=l. Esto se lee como: Como n tiende al infinito, tiende a l.

Además, si para una sucesión an se podemos encontrar un numero M positivo, tal que, | an | M n N entonces la sucesión { an } se dice que es cerrada.

Similarmente, las sucesiones pueden estar creciendo o decreciendo.

Algunas de las propiedades generales de los Límites de una Sucesión incluyen:

1).Los Límites de las sucesiones de origen convergentes son únicos.

2). Una sucesión de origen convergente es siempre cerrada y viceversa.

3). En el caso de las sucesiones {an} n 1, junto con {bn} n 1 son de origen convergente y x e y son números reales, en ese caso, la sucesión { xan + ybn }n 1 es también convergente.

4). Similarmente, si las sucesiones {an} n 1 junto con {bn} n 1 son de origen convergente y x e y son números reales, en ese caso, la sucesión { xan . ybn }n 1 es también convergente. Obtenemos,

5). En el caso de la sucesión {an}, n 1 tiene un origen convergente con la condición que an 0 y an 0 para n 1, entonces la secuencia del tipo es también convergente.

Los límites de las sucesiones estándares pueden ser útiles para facilitar el cálculo. Algunos de estos son:

1). = 0

2). = 0 | r | < 1.

3). = 0 donde sn = a + ar + ar2 + …..+ 

Este límite es conocido como serie infinita geométrica con el primer término “a” y la razón común “r”. Para captar efectivamente el concepto de las propiedades y las características de los límites de sucesiones, observemos un ejemplo en el que se requiere demostrar que para un número x, donde 0 <x <1 xn = 0

Dado que 0 < x < 1, por tanto la sucesión xn es cerrada y decreciente. De acuerdo a la segunda propiedad citada arriba, esta es convergente. Entonces, xn = L

3.2 Limite de una función de variable real 

Se le llama función real de variable real a toda la función definida de un subconjunto D de los números reales, en el conjunto R de los números reales, tal que a cada elemento x de D le corresponde uno y sólo un elemento y de R:

f:D————->R

x————->x2.

Para que una función quede correctamente definida es necesario determinar:

1. El conjunto inicial o dominio de la función.

2. El conjunto final o imagen de la función.

3. La regla por la cual se asigna a cada elemento del conjunto origen un solo elemento del conjunto imagen.

Así, por ejemplo, la función definida por:

f:R ——–>R

x———>x2.

Asigna a cada número real su cuadrado.

Tiene por conjunto origen o campo de existencia todos los números reales, pues dado cualquier número real x, siempre es posible calcular su cuadrado, siendo el resultado otro número real. Tiene por conjunto imagen todos los números reales positivos, puesto que el cuadrado de un número siempre es positivo:

lim(f)=R+.

La regla de asignación es: “Dado cualquier número real x, calcular su cuadrado para obtener la imagen”. El límite de una función de variable real es un concepto importante en el cálculo. Según este, si F es la función de una variable real r, en ese caso, el límite de F como r se aproxima a x existe, si existe otro número real R entonces para un número positivo conocido Descripción: http://mitecnologico.com/igestion/uploads/Main/cal12.jpg , existe otro número delta, tal que | F® - N | ‹ para todo r que satisfaga | r - x | < . Esto es,

 y   son letras de Grecia utilizadas tradicionalmente, a las cuales se les llama como descripción de límites épsilon-delta. Puede ser el caso cuando la función F satisface \ limita_{r\a\x} la definición en una sola dirección en la recta numérica real. Suponga que satisface la existencia de límites desde la izquierda. En ese caso, puede ser representada como este caso puede ser leído como ‘la existencia de límites del lado izquierdo’. Del mismo modo, los límites del lado derecho pueden ser demostrados como

Sin embargo, no se puede decir que el límite existe enteramente hasta que ambos límites de lado izquierdo y derecho persistan y se conviertan iguales.

Mientras se resuelve un problema “ límite de una función de variable real “ se debe hacer énfasis principalmente en el cálculo del rango del límite y no en identificar si el límite existe o no.

El límite de una función de variable real se puede definir en el infinito si la recta numérica es considerada extensible. Si F® es la función, entonces, el límite infinito de F se puede representar como que existen algunas propiedades que valen la pena considerar mientras se trata con el concepto de límite de la función de variable real F:

1). El límite de F se dice que existe cuando los límites del lado derecho y del lado izquierdo existen para la función correspondiente.

2). Se dice que F es continua en un punto particular A solo si en el caso el límite F( r ) como r se mueve hacia A subsiste y es equivalente a f(A).

3). Si el límite de la función F® como r se mueve hacia A es L1 y el límite de otra función H® como r se mueve hacia A es L2, entonces, el límite de F® + H® como se mueve hacia A es L1 + L2.

4). El límite de F debe ser compatible con las operaciones aritméticas con la condicionante que el límite del lado derecho exista.

La definición y sus propiedades pueden ser más profundamente ilustradas con la ayuda de un ejemplo. Consideremos una función

        F® = La función puede ser simplificada como:

       

        F® = (r + 2) (r - 2)

                      (r – 2)

        F® = r + 2, r   2

Es decir la línea r + 2 con el punto ( 2, 4 ) son los puntos faltantes.

Se puede observar que r = 2 no se encuentra en el dominio de F y 4 no está en el rango correspondiente. Por lo cual, al poner r cerca del 2, obligará a F hasta el punto (2, 4). Esto es, de acuerdo a la definición, si un número real es dado, entonces se necesita encontrar otro número , tal que, < . Entonces, este puede ser probado como:

    Si |r −2| <

    2+   < r < 2 -

    2 -   + 2< r + 2 < 2 +   + 2

    4 -   < r + 2 < 4 +

    4 -  < r + 2 < 4 + 

    |(r + 2) - 4| <  

3.3 Cálculo de limites 

Si f(x) es una función usual (polinómicas, racionales, radicales, exponenciales, logarítmicas, etc.) y está definida en el punto ha, entonces se suele cumplir que:

                                                               

Es decir: Para calcular el límite se sustituye en la función el valor al que tienden las x.

                             

                             

                             

No podemos calcular porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.

Todos nosotros hemos leído en las matemáticas básicas que si el valor del denominador es cero, entonces obtendremos un valor indefinido como producto. Pero en el caso del cálculo, podemos obtener una solución aunque el valor del denominador sea cero.

Para entender el concepto, mire el ejemplo dado a continuación, f(x) = x3/ x

Si lo resolvemos tenemos f(x) = x2 como respuesta. El gráfico de esta función es una parábola, como se muestra debajo, ahora bien, si x alcanza el valor de cero en algún punto entonces tenemos una salida indefinida.Utilizando el cálculo obtenemos el valor de la ecuación para un valor algo más grande y para un valor algo menor que cero. Este es el concepto detrás de los límites.

El concepto de límite es que al llegar más y más cerca de un valor específico de x, el valor de la función también comienza a resolverse en torno a un valor específico. De este modo podemos calcular el valor de la función para algunos valores que están muy cerca de cero.

Esto proporcionará un resultado de valor aproximado para la función dada y por tanto no obtendremos un valor indefinido como valor de salida de la función. Para el ejemplo ilustrado arriba tendríamos cero como salida si el valor del denominador es casi igual a cero. Esto es debido a que el valor de salida de la función se aproxima al valor de cero a medida que el valor de entrada de la función llega a cero. Se puede observar claramente en el gráfico de la función.

Sin embargo no siempre es el caso que tanto el valor de entrada como el valor salida de la función alcancen el mismo valor. El cálculo ayuda en la determinación de la salida de una función no habiéndose dado un valor indeterminado de la función como salida. Esto hace el concepto de límite distinto de simple álgebra.

No es esencial que el valor de la función sea indefinido solamente para cero. Funciones diferentes tienen valores de entrada diferentes para los cuales la función es indefinida. Por lo tanto el límite puede ser leído “se define límite como la entrada tiende a una variable que hace la función salida indefinida”.

Existen otras propiedades importantes también que sin embargo no podemos abordar aquí.

 Veamos ahora un ejemplo:

limx2 (3×2 – 4x + 5)

= limx2 (3×2) - limx2 (4x) + limx2 (5)

= 3limx2 (x2) - 4limx2 (x) + limx2 (5)

= 3(2)2- 4(2) + 5

= 12 – 8 + 5

= 9

3.4 Propiedades de los limites

                                                      

3.5 Limites laterales

 De manera similar, x puede aproximarse a c tomando valores más grandes que éste (derecha): O tomando valores más pequeños (izquierda), en cuyo caso los límites pueden ser escritos como: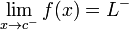

Si los dos límites anteriores son iguales:

Entonces L se pueden referir como el límite de f(x) en c. Dicho de otro modo, si estos no son iguales a L entonces el límite, como tal, no existe.

  

                                          

3.6 Limites infinitos y limites al infinito

Si una variable independiente x está creciendo indefinidamente através de valores positivos se escribe y si decrece a través de valores negativos se denota como 

Similarmente cuando una función f(x) crece indefinidamente y toma valores positivos cada vez mayores, es escribe ƒ(x)→ + ∞ y si decrece tomando valores negativos se escribe  ƒ(x)→ - ∞. Infinito, la palabra aparece regularmente en los conceptos Matemáticos, esta es básicamente sólo una idea y no un número. Una cantidad extremadamente grande la cual no está definida puede ser considerada como infinito. Cuando se calcula el límite de una fracción, en la que el numerador se acerca a una cantidad positiva o negativa, si el denominador se mueve hacia 0, entonces en ese caso se dice que el límite es inexistente. Con el fin de explicar el comportamiento de tales funciones, decimos que

   

                                      

Esto indica que el límite de F® es un número desconocido de gran tamaño. Este tipo de límites es conocido como Límite Infinito. Los límites infinitos significan básicamente que el límite es imaginario, es decir, el valor de la función se puede hacer tan grande como queramos tomando los valores de r suficientemente cerca de 0.

Por ejemplo: una función x = 3y tiene límites infinitos. A medida que y aumenta, 3y también aumenta y cuando y se acerca al infinito, el límite de 3y se vuelve infinito.

                                      

Además la definición de límite infinito puede ser girada para un límite de un solo lado. El grafico correspondiente de la función g(x) =  

que también posee límites infinitos puede ser dibujada como:

                                           

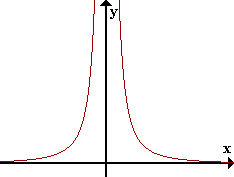
x −1 −0.1 −0.01 −0.001 0 g(x) 1 100 10,000 1,000,000 indefinido

Un concepto casi similar es el de “limites al infinito”. En este cuando la función de una variable y aumenta ilimitadamente entonces esta es mostrada como

                                                           

De manera similar, cuando y cae de manera ilimitada, entonces esta es mostrada como

                                                           

El concepto principal de límites al infinito yace en dos puntos.

1). Cuando k es un número no negativo, entonces 

                                                         

2). Cuando k es un número no negativo, entonces 

                                                          

Encontrar el límite de un número racional al infinito es un caso especial en este concepto. Una regla sencilla para determinar el límite al infinito de tales números es considerando la variable, tanto en el numerador y en el denominador, que tenga el mayor exponente. Ahora bien, los límites pueden ser evaluados en base a las siguientes reglas:

1). Si el numerador con el más alto exponente va junto al denominador con el más alto exponente, en ese caso, el limite al infinito y el infinito negativo es la proporción de ambos coeficientes de mayor término.

2). Al dividir el numerador con el denominador, si el exponente resultante en la variable queda igual, en ese caso, el límite al infinito y el infinito negativo son infinitos. Si resulta impar, en ese caso, el límite al infinito es infinito y el infinito negativo es infinito negativo. Sin embargo, en ambas condiciones, el numerador debe tener el término más alto.

3). En la fracción impropia, es decir, en la cual el denominador contiene el término más alto, el límite al infinito y el infinito negativo es 0.

Los límites infinitos siguen unas propiedades importantes al infinito, las cuales son:

1.-     

En caso, que r sea grande, entonces el recíproco de r será extremadamente pequeño y en el caso que r aumente rápidamente, entonces  

              

Disminuirá en una proporción igual y eventualmente llegará cerca de 0.

2.-. Del mismo modo, si r se convierte grandemente negativo,  se convertirá menos negativo y también se aproximará más a 0.

3.-  Además, un ejemplo similar ocurre cuando r es elevado a algún exponente, es decir,

3.7 Asintotas

Una línea recta que se aproxima continuamente a otra función o curva, que la distancia entre las 2 tiende a 0 a medida que se extiende indefinidamente.



También se puede decir que es la curva la que se aproxima a la recta, o que en ambas presentan un comportamiento asintótico.

                   

Asíntota Vertical (AV)



La recta x=a es asíntota vertical de f(x) si limx->a+
f(x) = inf o limx->a- f(x) = inf.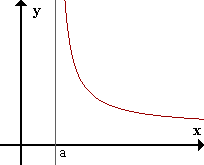

                          

Asíntota Horizontal (AH)



La recta y=b es asíntota horizontal de f(x) si limx->inf
f(x) = b.

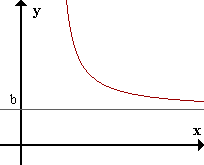
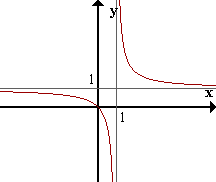
Un ejemplo que podemos tener es: 



f(x) = x/(x-1)limx->1+ f(x) = +inf



limx->1- f(x) = -inf=> x=1 es AV de f(x)



limx->inf f(x) = 1



=> y=1 es AH de f(x)

3.8 Funciones continuas y discontinuas en un punto y en un intervalo

Funciones continuas: Una función es continua en un punto si existe límite en él

y coincide con el valor que toma la función en ese punto. Una idea intuitiva de función continua se tiene al considerar que su gráfica es continua, en el sentido que se puede dibujar sin

levantar el lápiz de la hoja de papel.


Continuidad de una función en un punto. 

Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:


1. Que el punto x= a tenga imagen.



2. Que exista el límite de la función en el punto x = a.



3. Que la imagen del punto coincida con el límite de la
función en el punto. Si una función no es continua en un punto x=a, diremos que

es discontinua en dicho punto.



Una función es continua por la derecha en un punto si
existe el límite por la derecha en él y coincide con el valor que toma la
función en ese punto, es decir


Una función es continua por la izquierda en un punto si
existe el límite por la izquierda en él y coincide con el valor que toma la
función en ese punto.

Discontinuidades



1.- Una función es discontinua en un punto cuando no existe
límite en él o, existiendo, no coincide con el valor de la función en el mismo.


2.- Una función tiene una discontinuidad evitable en un
punto cuando existe límite en él y no coincide con el valor de la función en el
mismo.El valor que deberíamos dar a la función en dicho punto para que fuera
continua en él se llama verdadero valor de la función en el mismo.


3.- Una función tiene una discontinuidad inevitable.






















3.9 Tipos de discontinuidades







                                                   




Discontinuidad evitable









Si una función tiene límite en un punto, pero la función en
ese punto tiene un valor distinto:




               




o no existe:




              








se dice que la discontinuidad es evitable, asignando a la función,
en ese punto, el valor del límite:







               






Discontinuidad esencial o no evitable







Se dice que una función presenta una discontinuidad
esencial cuando se produce algunas de las siguientes situaciones:




Existen los límites laterales pero no coinciden. Alguno de los límites laterales o ambos son infinitos. No existe alguno de los límites laterales o ambos.Discontinuidad de primera especie




En este tipo de discontinuidad existen tres tipos:



DE SALTO FINITO




Existen el límite por la derecha y por la izquierda del
punto, su valor es finito, pero no son iguales:





               

como en el caso de que el límite por la izquierda sea infinito y por la derecha finito:







              




Se dice que la discontinuidad es de salto infinito.

DISCONTINUIDAD ASINTÓTICA


Si los dos límites laterales de la función en el punto x= a

son infinitos:


              

A este tipo de discontinuidad de primera especie se le
llama discontinuidad asintótica, siendo x= a la asíntota.


Discontinuidad de segunda especie. Si la función no existe en uno de los lados del punto, o no existen alguno, o ambos, de los límites laterales de la función en ese punto,

se dice que la función presenta una discontinuidad de segunda especie en ese
punto.