DERIVADAS
4.1 Conceptos de incremento y de razón de cambio La
derivada de una función
4.2 La interpretación geométrica de la derivada
4.3 Concepto de diferencial Interpretación geométrica de
las diferenciales
4.4 Propiedades de la derivada
4.5 Regla de la cadena
4.6 Formulas de derivación y formulas de diferenciación
4.7 Derivadas de orden superior y regla L Hopital
4.8 Derivada de funciones implícitas
4.1 Conceptos de incremento y de razón de cambio La derivada de una función
INCREMENTO:
Cuando una cantidad variable pasa de un valor inicial a
otro valor, se dice que ha tenido un incremento. Para calcular este incremento
basta con hallar la diferencia entre el valor final y el inicial. Para denotar
esta diferencia se utiliza el símbolo ∆x, que se lee "delta x". El
incremento puede ser positivo o negativo, dependiendo de si la variable aumenta
o disminuye al pasar de un valor a otro. Por ejemplo, si el valor inicial de
una variable x, x1, es igual a 3, y el valor final x2 es igual a 7, el
incremento ∆x = x2 - x1 = 7 - 3 = 4: la variable se ha incrementado
positivamente en 4 unidades. En cambio, si el valor inicial es 7 y el valor
final 3, ∆x = x2 - x1 = 3 - 7 = -4: la variable ha tenido un incremento
negativo (decremento) de 4 unidades.
RAZON DE CAMBIO:
- El tamaño de una población (peces, ratas, personas,
bacterias,…)
- La cantidad de dinero en una cuenta en un banco
- El volumen de un globo mientras se infla
- La distancia t recorrida en un viaje después del comienzo
de un viaje
El cambio en Q desde el tiempo t hasta el tiempo t+∆t, es
el incremento
¨Q¨ es creciente en el instante t si
¨Q¨ es decreciente en el instante t si
La derivada de cualquier función, no solamente una función
del tiempo, puede interpretarse como una razón de cambio instantánea con
respecto de la variable independiente. Si y=f(x), entonces la razón de cambio
promedio de y (por un cambio unitario en x) en el intervalo [x,x+∆x] es el
cociente.
mt = f'(a)
Dada la parábola f(x) = x2, hallar los puntos en los que la
recta tangente es paralela a la bisectriz del primer cuadrante.
La bisectriz del primer cuadrante tiene como ecuación y =
x,
por tanto su pendiente es m = 1.
Como las dos rectas son paralelas tendrán
la misma pendiente, así que:
4.2 La interpretación geométrica de la derivada

Cuando h tiende a 0, el punto Q tiende a confundirse con el
P. Entonces la recta secante tiende a ser la recta tangente a la función f(x)
en P, y por tanto el ángulo α tiende a ser β.


Ejemplos:
Dada f(x) = x2, calcular los puntos en los que la recta
tangente es paralela a la bisectriz del primer cuadrante. La ecuación de la bisectriz del primer cuadrante es y = x
por tanto su pendiente es m= 1.
Como las dos rectas son paralelas tendrán la misma
pendiente, así que:
f'(a) = 1.
Dado que la pendiente de la tangente a la curva es igual a
la derivada en el punto x = a.




Dada la curva de ecuación f(x) = 2x2 − 3x − 1, halla las
coordenadas de los puntos de dicha curva en los que la tangente forma con el
eje OX un ángulo de 45°.






Determinar los valores del parámetro b, para qué las
tangentes a la curva de la función f(x) = b2x3 + bx2 + 3x + 9 en los puntos de
abscisas x = 1, x = 2 sean paralelas.
Para que sean paralelas se tiene que cumplir que las
derivadas en x = 1 y x = 2 sean iguales.
f'(1) = f'(2)
f'(x) = 3b2x2 + 2bx + 3
f'(1) = 3b2 + 2b + 3
f'(2) = 12b2 + 4b + 3
3b2 + 2b + 3 = 12b2 + 4b + 3
9b2 + 2b = 0
b = 0 b = −2/9
Interpretación física de la derivada
Velocidad media. La velocidad media es el cociente entre el espacio
recorrido (Δe) y el tiempo transcurrido (Δt).


Velocidad instantánea
La velocidad instantánea es el límite de la velocidad media
cuando Δt tiende a cero, es decir, la derivada del espacio respecto al tiempo.


Ejemplos:
La relación entre la distancia recorrida en metros por un
móvil y el tiempo en segundos es e(t) = 6t2. Calcular:
1 la velocidad media entre t = 1 y t = 4.
La velocidad media es el cociente incremental en el
intervalo [1, 4].

2 La velocidad instantánea en t = 1.
La velocidad instantánea es la derivada en t = 1.



4.3 Concepto de diferencial Interpretación geométrica de las diferenciales
En el campo de la matemática llamado cálculo, el
diferencial representa la parte principal del cambio en la linealización de
unafunción y = ƒ(x) con respecto a cambios en la variable independiente. El
diferencial queda definido por la expresión como si la derivada dy/dx
representara el cociente entre la cantidad dy y la cantidad dx. Se puede
también expresar como el significado preciso de estas expresiones depende del
contexto en las cuales se las utilice y el nivel de rigor matemático requerido.
Según consideraciones matematicas rigurosas modernas, las cantidades dy y dx
son simplemente variables reales y son manipuladas como tales. El dominio de
estas variables puede tomar una significación geométrica particular si el
diferencial es considerado como una forma diferencial, o significancia
analítica si el diferencial es considerado como una aproximación lineal del
incremento de la función. En aplicaciones físicas, a menudo se requiere que las
variables dx y dy sean sumamente pequeñas (infinitesimales).
Definición
El diferencial está definido en los tratamientos modernos
del cálculo diferencial de la siguiente manera.1 El diferencial de una
funciónƒ(x) de una única variable real x es la función df de dos variables
reales e independientes x y Δx dada por:
Uno, o los dos, argumentos pueden ser suprimidos:
ej., se puede ver df(x) o simplemente df. Si y = ƒ(x), el
diferencial también puede ser escrito dy. Dado que dx(x, Δx) = Δx es
convencional escribir dx = Δx, de manera que la igualdad se mantiene.
Interpretación geométrica del diferencial
Interpretación geométrica del diferencial de una función en
un punto.
El diferencial se puede tomar en el sentido geométrico como
la elevación de la tangente desde el punto en que se toma el diferencial.
Recuérdese que la derivada de la función en el punto es la
pendiente de la recta tangente a la función en el punto, como sabemos que la
tangente de un ángulo es igual al cociente entre el cateto opuesto (incremento
de y) y el cateto contiguo (incremento de x) de un hipotético triángulo
rectángulo, sólo hay que despejar el incremento de y que equivale a nuestro
diferencial.
Vista geométricamente, la elevación se produce
verticalmente a partir del punto en que se toma el diferencial. El
incremento que se tome representará el
alejamiento horizontal que haga desde el punto en cuestión. Así la elevación de la tangente que se obtenga como
resultado dependerá del punto en cuestión y del alejamiento horizontal que se
tomen, que en la formulas matemáticas están definidos respectivamente por ¨y
4.4 Propiedades de la derivada
Derivada una función constante
La derivada de una función constante es cero.
Ejemplo
Si  , entonces
, entonces

 , entonces
, entonces
Derivada de una suma de funciones
La derivada de la suma de dos funciones es igual a la suma de las derivadas de dichas funciones:
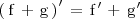
Este resultado, se puede ampliar a cualquier número de funciones:

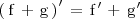

Derivada de una diferencia de funciones
La derivada de la diferencia de dos funciones es igual a la diferencia de las derivadas de dichas funciones:
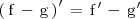
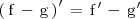
Ejemplo

Derivada de un producto de funciones
La derivada del producto de dos funciones,  y
y 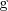 , viene dada por la fórmula:
, viene dada por la fórmula:
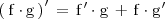
 y
y 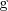 , viene dada por la fórmula:
, viene dada por la fórmula: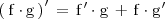
Ejemplo

Observese que  y que la derivada de
y que la derivada de  es precisamente
es precisamente  .
.

 y que la derivada de
y que la derivada de  es precisamente
es precisamente  .
.Derivada de un cociente de funciones
La derivada del cociente  viene dada por la fórmula:
viene dada por la fórmula:
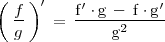
 viene dada por la fórmula:
viene dada por la fórmula: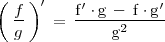
Ejemplo






4.5 Regla de la cadena
En cálculo, la regla de la cadena es una fórmula para la derivada de la composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas cuando existe composición de funciones.
Descripción de la regla:En términos intuitivos, cola si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto a x puede ser calculada con el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.
Descripción algebraica:En términos algebraicos, la regla de la cadena (para funciones de una variable) afirma que si
 es diferenciable en
es diferenciable en  y
y  es una función diferenciable en
es una función diferenciable en  , entonces la función compuesta
, entonces la función compuesta  es diferenciable en
es diferenciable en  y
y
Notación de Leibniz:
Alternativamente, en la notación de Leibniz, la regla de la cadena puede expresarse como:

donde  indica que g depende de f como si ésta fuera una variable.
indica que g depende de f como si ésta fuera una variable.
 indica que g depende de f como si ésta fuera una variable.
indica que g depende de f como si ésta fuera una variable.
Demostración de la regla de la cadena

Esto es entonces

Aplicando la definición de derivada se tiene
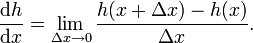
Donde queda

Equivalentemente, multiplicando y dividiendo entre 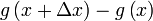 (esta demostración solo vale cuando
(esta demostración solo vale cuando 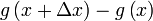 es distinto de cero , por ejemplo si g(x) fuera constante no se cumple)
es distinto de cero , por ejemplo si g(x) fuera constante no se cumple)
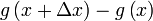 (esta demostración solo vale cuando
(esta demostración solo vale cuando 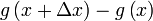 es distinto de cero , por ejemplo si g(x) fuera constante no se cumple)
es distinto de cero , por ejemplo si g(x) fuera constante no se cumple)
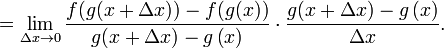
 cqd
cqd- Ejemplos de aplicación
- Ejemplo conceptual
Este cálculo es una aplicación típica de la regla de la cadena.
Ejemplo algebraico:
Por ejemplo si
 es una función derivable de
es una función derivable de  y si además
y si además 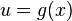 es una función derivable de
es una función derivable de  entonces
entonces 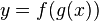 es una función derivable con:
es una función derivable con:
o también
![\frac{d}{dx} [f(g(x))]=f '(g(x))\cdot g'(x)](http://upload.wikimedia.org/math/8/5/8/858ff94f3748b67089b3b3a0f4048bcf.png)
Ejemplo 1

y queremos calcular: 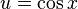
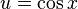
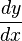
Por un lado tenemos:

y

si:

entonces:

Si definimos como función de función:

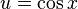
resulta que:

 con el mismo resultado.
con el mismo resultado.
Ejemplo 2
Tenemos 

la cual se puede definir como función compuesta. Si desglosamos la función compuesta quedaría:
 , cuyas derivadas serían:
, cuyas derivadas serían:
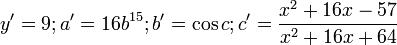
Con la regla de la cadena, esto sería:

Los cuales corresponden a las derivadas anteriormente extraídas.


Se reemplazan las letras b y c por sus valores NO derivados, no confundir.
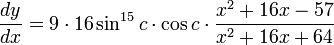
Y luego se obtiene la derivada.

 , cuyas derivadas serían:
, cuyas derivadas serían: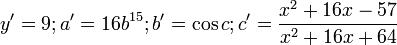
Con la regla de la cadena, esto sería:

Los cuales corresponden a las derivadas anteriormente extraídas.


Se reemplazan las letras b y c por sus valores NO derivados, no confundir.
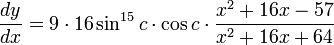
Y luego se obtiene la derivada.

Derivadas de orden superior:
Las fórmulas de Faà di Bruno generalizan la regla de la cadena a derivadas de orden superior. Algunas de ellas son:




4.6 Formulas de derivación y formulas de diferenciación
Formulas de Derivación
I dc = 0
La derivada de una constante es cero
II dx = 1
La derivada de una variable con respecto a si misma es la unidad.
III d ( u + v – w ) = du + dv - dw
La derivada de la suma algebraica de un numero finito n de funciones es igual a la suma algebraica de las derivadas de las funciones
IV d ( cv ) =c. dv
La derivada del producto de una constante por una función es igual al producto de la constante por la derivada de la función
V d (uv) = u dv + v du
La derivada de un producto de dos funciones es igual al producto de la primera funcion por la derivada de la segunda, mas el producto de la segunda por la derivada de la primera.
VI d (un) = nun-1 du
La derivada de la potencia de una función de exponente constante es igual al producto del exponente por la función elevada a un exponente disminuido en una unidad y por la derivada de la función.
VIa d (xn ) = nxn - 1
V d (uv) = u dv + v du
La derivada de un producto de dos funciones es igual al producto de la primera funcion por la derivada de la segunda, mas el producto de la segunda por la derivada de la primera.
VI d (un) = nun-1 du
La derivada de la potencia de una función de exponente constante es igual al producto del exponente por la función elevada a un exponente disminuido en una unidad y por la derivada de la función.
VIa d (xn ) = nxn - 1
Cuando v = x se convierte en la expresion anterior
VII d ( uv ) = v.du - u.dv.
v2 La derivada de un cociente de funciones es igual al producto del denominador por la derivada del numerador, menos el producto del numerador por la derivada del denominador, todo dividido por el cuadrado del denominador
VIIa d ( u/c ) = du/ c
La derivada del cociente de una funcion dividida por una constante es igual a la derivada de la funcion dividida por la constante

Sean a, b, e y k constantes (números reales) y consideremos a: u(x) y v(x) como funciones.
En adelante, escribiremos u y v con el fin de simplificar.
Derivada de una constante

Derivada de x

Derivada de la función lineal

Derivada de una potencia

Derivada de una raíz cuadrada

Derivada de una raíz

Derivada de una suma

Derivada de una constante por una función

Derivada de un producto

Derivada de una constante partida por una función

Derivada de un cociente

Derivada de la función exponencial

Derivada de la función exponencial de base e

Derivada de un logaritmo

Como  , también se puede expresar así:
, también se puede expresar así:
 , también se puede expresar así:
, también se puede expresar así:
Derivada del logaritmo neperiano

Derivada del seno

Derivada del coseno

Derivada de la tangente

Derivada de la cotangente

Derivada de la secante

Derivada de la cosecante

Derivada del arcoseno

Derivada del arcocoseno

Derivada del arcotangente

Derivada del arcocotangente

Derivada del arcosecante

Derivada del arcocosecante

Derivada de la función potencial-exponencial

Regla de la cadena

Derivadas implícitas

4.7 Derivadas de orden superior y regla L Hopital
Derivadas de orden superior
Sea f(x) una función diferenciable, entonces se dice que f
'(x) es la primera derivada de f(x). Puede resultar f '(x) ser una función
derivable, entonces podriamos encontrar su segunda derivada, es decir f(x).
Mientras las derivadas cumplan ser funciones continuas y que sean derivables
podemos encontrar la n-ésima derivada. A estas derivadas se les conoce como
derivadas de orden superior.
Notación
Se utiliza la siguientes notaciones para representar las derivadas de orden superior

Se utiliza la siguientes notaciones para representar las derivadas de orden superior

Ejemplo 1:
Ejemplo 2:
Ejemplo 2:
Ejemplo 3:
Ejemplo 4:
Ejemplo 5:
Regla de L'Hôpital
Si  , en donde f y g son derivables en un entorno de a y existe
, en donde f y g son derivables en un entorno de a y existe  este límite coincide con
este límite coincide con
 , en donde f y g son derivables en un entorno de a y existe
, en donde f y g son derivables en un entorno de a y existe  este límite coincide con
este límite coincide con .
.
La regla de L'Hôpital se aplica directamente en las indeterminaciones:

Ejemplos






Indeterminación infinito menos infinito


Indeterminación infinito menos infinito




Indeterminación cero por infinito




Indeterminaciones
En las sin determinaciones cero elevado cero, infinito elevado a cero y uno elevado a infinito; se realiza en primer lugar las siguientes operaciones: 



Ejemplos
Ejercicios
Aplicando las propiedades de los logaritmos en el segundo miembro tenemos:
4.8 Derivada de funciones implícitas
Derivada de funciones implícitas. La derivada de la función implícita definida mediante la ecuación
definida mediante la ecuación  puede calcularse: o bien despejando la y , o bien, mediante la siguiente fórmula:
puede calcularse: o bien despejando la y , o bien, mediante la siguiente fórmula: , siempre que
, siempre que 
Las derivadas de orden superior de una función implícita se pueden calcular mediante la derivación sucesiva de la fórmula anterior, considerando y como función de x.
Las derivadas parciales de una función implícita de dos variables  definida mediante la ecuación
definida mediante la ecuación  puede calcularse mediante las fórmulas:
puede calcularse mediante las fórmulas:
Dada la ecuación  Si el punto
Si el punto  cumple la ecuación
cumple la ecuación  , la función F tiene derivadas parciales continuas en un entorno de
, la función F tiene derivadas parciales continuas en un entorno de  y
y  entonces la ecuación
entonces la ecuación  define una función explícita
define una función explícita  en un entorno de
en un entorno de con
con
Dada la ecuación  Si el punto
Si el punto  cumple la ecuación
cumple la ecuación  la función F tiene derivadas parciales continuas en un entorno de
la función F tiene derivadas parciales continuas en un entorno de  y
y  entonces la ecuación
entonces la ecuación  define una función explícita
define una función explícita  en un entorno de dicho punto.
en un entorno de dicho punto.
—————————————————————————————————
22. Calcula y', siendo
Solución:
Tenemos: 
hallamos las derivadas parciales:
Por lo tanto:
—————————————————————————————————
23. Calcula
Solución:
Tenemos: 
hallamos las derivadas parciales:
Por lo tanto:
—————————————————————————————————
24. Demuestra que la ecuación
Solución:
a) Existencia de la función explícita:
Consideramos la función:  tenemos:
tenemos:
F es diferenciable con continuidad en  y por lo tanto en un entorno de (1, 1)
y por lo tanto en un entorno de (1, 1)
Luego, de acuerdo con el teorema de existencia de funciones implícitas existe  en un entorno de 1 con
en un entorno de 1 con 
b) Cálculo de y'(1)
Derivamos la ecuación  teniendo en cuenta que y es función de x
teniendo en cuenta que y es función de x 
c) Cálculo de y''(1)
Derivando la ecuación se tiene.
se tiene.
Este caso particular también se podía haber resuelto despejando  y eligiendo el signo + ya que
y eligiendo el signo + ya que
—————————————————————————————————
25. Calcula dz en la ecuación
Solución:
Consideramos la función: 
Hallamos las derivadas parciales
Con lo cual
Con lo que resulta:





























































No hay comentarios:
Publicar un comentario