Unidad 2

Unidad 2

2.1 Concepto de variable, función, dominio, codominio, y recorrido de una función

2.2 Función inyectiva, suprayectiva, y biyectiva

2.3 Función de variable real y su representación gráfica

2.4 Funciones algebraicas: función polinomial, racional, e irracional

2.5 Funciones trascendentes: funciones trigonométricas y funciones exponenciales

2.6 Función definida por mas de una regla de correspondencia, función valor absoluto

2.7 Operaciones con funciones: adición, multiplicación, composición

2.8 Función inversa, logarítmica y trigonométricas inversas

2.9 Funciones con dominio en los números naturales y recorrido en los números reales: las sucesiones infinitas

2.10 Función implícita

2.1 Concepto de variable, función, codominio, y recorrido de una función

Variable: Una variable es la expresión simbólica representativa de un elemento no especificado comprendido en un conjunto. Este conjunto constituido por todos los  elementos o variables, que pueden sustituirse unas a otras es el universo de variables. Se llaman así porque varían, y esa variación es observable y medible.

Función: En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).  En lenguaje cotidiano o más simple, diremos que las funciones matemáticas equivalen al proceso lógico común que se expresa como “depende de”. Las funciones matemáticas pueden referirse a situaciones cotidianas, tales como: el costo de una llamada telefónica que depende de su duración, o el costo de enviar una encomienda que depende de su peso.

 Dominio: En su forma más simple el dominio son todos los valores a los que aplicar una función, y el rango son los valores que resultan.

Codominio: En matemáticas, el codominio o contradominio (también denominado conjunto final, recorrido o conjunto de llegada) de una función 

Recorrido de una función: El recorrido de una función es el conjunto de valores que toma la variable dependiente,  es decir, todos los valores de la variable dependiente que son imagen de algún valor de la variable independiente

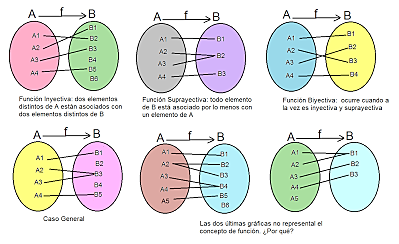
2.2 Función inyectiva, suprayectiva y función biyectiva.

Función inyectiva: Una función es inyectiva si a cada valor del conjunto (dominio) le corresponde un valor distinto en el conjunto de. Es decir, a cada elemento del conjunto A le corresponde un solo valor tal que, en el conjunto A no puede haber dos o mas elementos que tengan la misma imagen.

 

Función Suprayectiva: Una función es suprayectiva, si esta aplicada sobre todo el condominio, es decir, cuando la imagen, o en palabras mas sencillas, cuando cada elemento de Y es la imagen de como mínimo un elemento de X

Función biyectiva: Una función es biyectiva si al mismo tiempo inyectiva y suprayectiva.

Para ser mas claro se dice que una función es biyectivaa cuando todos los elementos del conjunto de partida en este caso (x) tienen una imagen distinta en el conjunto de llegada, que es la regla de la función inyectiva. Sumándole que cada elemento del conjunto de salida le corresponde un elemento del conjunto de llegada en este caso Y que es la norma que exige la función suprayectiva.

2.3 Función de Variable Real y su Representación Gráfica

Cualquier función cuyo rango de conjunto incluya sólo números reales esllamada una función valorada real o simplemente una función real.

Especialmente estudiada bajo el cálculo, una función valorada real se centra en las integrales, las desigualdades en general y sus derivadas.

Una función racional, por ejemplo, cae bajo la categoría de una función valorada real.

Algunas de las funciones valoradas reales y sus gráficos se analizan a continuación:

1. Función Constante y Gráfico: Una función constante es una función f: X → Y, donde X e Y son subconjuntos de R y existe k como un elemento de Y tal que f(x) = k.

El gráfico formado para esta función es una línea recta paralela al eje X.

Si tenemos que k> 0 la línea estará por encima del eje x, sinola línea se formará por debajo del eje-x.

En el caso que k sea igual a cero la línea se superpone al eje-x.

Ejemplo, y = 12, en este caso una línea paralela al eje x que pasa por el 12vo punto formará la gráfica.

2. Función Identidad y Gráfico: Una función identidad es una función f: X → Y que tiene la propiedad f(x) = x se mantiene cierta a los elementos de X.

La gráfica de esta función es una línea recta que se traza en un ángulo de cuarenta y cinco grados con el eje x y se extiende en ambos planos negativos y positivos.

Tal función toma un elemento para sí mismo y nunca cambia su dominio. Ejemplo, f (x) = x, en este caso una línea en un ángulo de cuarenta y cinco grados pasa el eje x a travésdel origen y formará la gráfica.

2.4 Funciones algebraicas: función polinomial, racional, e irracional

Función polinomial:

Una función polinomial es una función en que f(x) es un polinomio en x.Una función polinomial de grado n es escrita como

Las funciones polinomiales están definidas y son continuas en todos los números reales.

Función lineal

f(x) = ax + b, a ≠ 0

1

Función cuadrática

f(x) = ax² + bx + c, a ≠ 0

2

Función cúbica

f(x) = ax³ + bx² + cx + d, a ≠ 0

3

Función cuártica

f(x) = ax⁴ + bx³ + cx² + dx + e, a ≠ 0

4

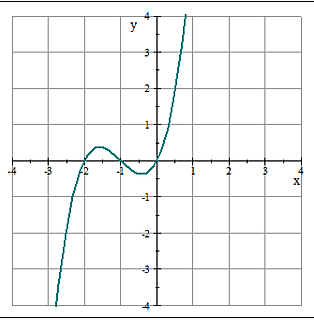
Función racional:

En matemáticas, una función racional de una variable es una función que puede ser expresada de la forma:

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen sudominio de definición en todos los valores de x que no anulen el denominador. Obviamente esta definición puede extenderse a un número finito pero arbitrario de variables, usando polinimios de varias variables

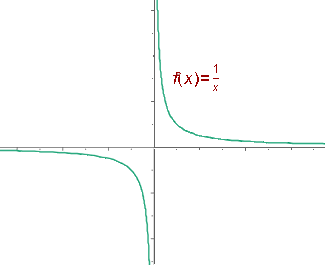
Función irracional:

Una función irracional es una función en cuya expresión analítica la variable dependiente x aparece debajo del símbolo de raíz.

En este apartado consideraremos únicamente funciones irracionales del tipo

f(x)=g(x)−−−−√n

con g(x) una función racional.

Si el índice n de la raíz es impar, es posible calcular la imagen de cualquier número real, siempre y cuando la expresión g(x) sea un número real, es decir, Dom(f)=Dom(g).

Si el índice n de la raíz es par, para poder calcular imágenes necesitamos que g(x) sea positiva o cero, ya que las raíces pares de un número negativo no son números reales. Por tanto el dominio de f son las soluciones de la inecuación g(x)≥0. En otras palabras, Dom(f)={x∈R∣g(x)≥0}.

Estudiemos ahora el caso más simple de función irracional: la función raíz cuadrada f(x)=x√.

Se trata de una función en que el índice de la raíz es 2. Por tanto, su dominio es el conjunto de soluciones de la inecuación x≥0. Así tenemos Dom(f)=[0,+∞) La imagen de la función raíz cuadrada es, como en el caso del dominio, el conjunto de los reales mayores o igual que cero, Im(f)=[0,+∞)

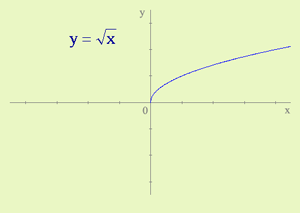
2.5 Funciones trascendentes: funciones trigonométricas y funciones exponenciales

Funciones trigonométricas:

Se asocian a cada número real, x, el valor de la razón trigonométrica del ángulo cuya medida en radianes es x.

Función seno

f(x) = sen x

Función coseno

f(x) = cosen x

Función tangente

f(x) = tg x

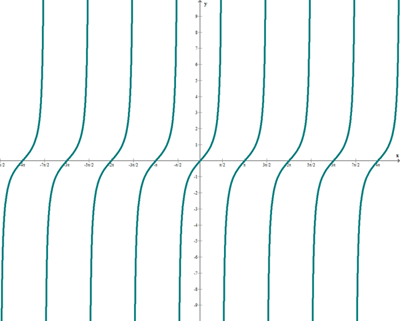
Función cosecante

f(x) = cosec x

Función secante

f(x) = sec x

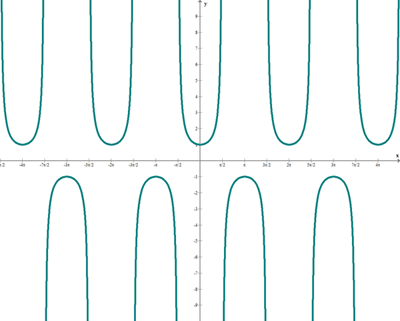
Función cotangente

f(x) = cotg x

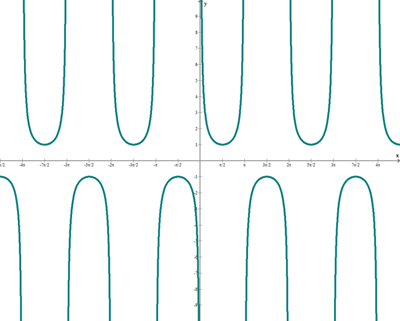
2.5 Funciones trascendentes: funciones trigonométricas y funciones exponenciales

Función exponencial

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.

2.6 Función definida por mas de una regla de correspondencia, función valor absoluto

Función a trozos es el nombre de una función que puede ser definida con la ayuda de múltiples funciones de correspondencia.

Una función f(x)=x⟶y es una función llamada función a trozos, si puede ser definida con ayuda de diferentes funciones lineales.

La gráfica de esta función también es definida por trozos, dependiendo el numero de ecuaciones que se utilicen para definir la función.

La función es llama así porque para definir esta función cambia según el valor de la variable de entrada.

La función de valor absoluto se transforma en función a trozos, siguiendo los siguientes pasos:

•          Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.
•          Se forman intervalos con el resultado de las raíces
•          Después definimos la función a trozos, tomando en cuenta que los intervalos en          donde la        x es negativa se le cambia el signo de la función.
• ·        Representamos la función.

EJEMPLO:

Veremos un ejemplo siguiendo los pasos antes citados.

F(x)=|x-3|

x-3                         x=3

2.7 Operaciones con funciones: adición, multiplicación, composición

Función de Adición, Función de Multiplicación, Función de Composición al igual que en cualquier otra cantidad matemática, es posible realizar operaciones básicas en las funciones.

Es posible sumar dos funciones, restar dos funciones, multiplicar dos funciones, dividir dos funciones y también hacer composiciones unas con las otras.

La suma de dos funciones está denotada por g(x) y f(x) es g + f. Consideremos dos funciones

 

La suma de dos funciones puede entenderse como graficar una de las funciones y tomar la función de ese gráfico como el eje x de la otra función.

Al igual que se suman dos funciones, también es posible multiplicar dos funciones.

Esto es similar a la suma de dos funciones, simplemente en lugar de ser una operación de suma uno necesita realizar la función de multiplicación.

La salida de la multiplicación de dos funciones producirá

El dominio de la función resultante será la intersección de los dominios de entrada de las funciones.

Como la suma de dos funciones, para llevar a cabo la multiplicación de dos funciones, uno simplemente tiene que multiplicar la salida de las dos funciones de entrada.

Tomemos como ejemplo la multiplicación de dos funciones,

g(x) = 3 √x y,

f(x) = √x

entonces, (g . f) (x) = (3 √x) . (√x)

La multiplicación de una función consigo misma se denota como,

f2(x) = f(x) . f(x)

también es posible multiplicar una función con cualquier cantidad escalar.

Esto es fácil de realizar, sólo multiplique cada una de las salidas con esa cantidad escalar.

La inserción de una de las funciones con otra función es llamada composición de la función.

De este modo, el rango de la función insertada se convertirá en el dominio de la función en la cual se insertó. También se conoce como la aplicación de una función sobre el resultado de otra función.

La composición de dos funciones siempre satisface la propiedad asociativa.

Esto es, si consideramos tres funciones f, g, h. La composición de estas tres funciones,

f 0 (g 0 h) = (f 0 g) 0 h

Aquí el paréntesis es utilizado para indicar la prioridad mientras se realiza la composición de las funciones.

La composición de funciones es también conmutativa, esto es, g 0 f = f 0 g. Pero esto no es cierto en todos los casos.

La composición de dos funciones se denota como

 

Tome como ejemplo:

g(x) = 2x + 3   f(x) = -x2 + 5

g(f(x)) = g(-x2 + 5) = 2(-x2 + 5) + 3 = −2×2 + 10 + 3 = −2×2 + 13

2.8 Función inversa, logarítmica y trigonométricas inversas

FUNCIONES INVERSA: Son dos funciones tales que a todo punto de la gráfica

de la primera función corresponde un punto de la gráfica de la segunda, de tal manera que la abscisa de cada punto de la primera es igual a la ordenada del punto correspondiente de la otra y viceversa; es decir, a todo punto de la primera curva corresponde, en la segunda, otro punto simétrico con respecto a la bisectriz del ángulo XOY.

FUNCIONES LOGARÍTMICAS: Una función se llama logarítmica cuando es de la forma y = log a x donde la base a es un número real y positivo pero distinto de 1

En la función logarítmica (cuando a > 1) cuanto mayor es la base del logaritmo, más cerca del eje X está.

Las funciones de la forma y = log a x cuando la base es mayor que la unidad (a > 1) tienen las siguientes características:

(tomando como ejemplo la función f (x) = log 5 x)

-Dominio: el dominio de la función son los reales positivos puesto que no existe el logaritmo de un número negativo. Dom (f) = R +

FUNCIONES TRIGONOMÉTRICAS INVERSAS: son las funciones que se definen a fin de extender la definición de las razones trigonométricas a todos los números reales.

surgen de una forma natural al estudiar el triángulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos cualesquiera de sus lados sólo dependen del valor de los ángulos del triángulo.

2.9 Funciones con dominio en los números naturales y recorrido en los números reales: las sucesiones infinitas

Funciones con Dominio en los Números Naturales y un Viaje a los Números Reales: Las Secuencias Infinitas

Considere un conjunto N, una función f: X , Y de la secuencia de números de N esta es conocida como función de sucesiones. El dominio de tales funciones se limita sólo a los números naturales. Las convenciones utilizadas para referirse a tales secuencias son,

La notación convenida para denotar una función de este tipo sería,

Una secuencia decreciente infinita es opuesta a la sucesión creciente infinita lo que significa que en el caso de una secuencia decreciente infinita el elemento subsecuente de la secuencia es más pequeño que el elemento que estaba ocurriendo antes que este en la secuencia, esto es un an+1 < an para todos los valores de n.

Mientras que una secuencia infinita monótona puede ser una que esté creciendo o decreciendo.

Otra categoría en la que una secuencia puede ser clasificada está basada en los límites de la secuencia, si estos se encuentran por encima o por debajo. Si existe un número M para el cual an <= M, para todos los valores de n, entonces tal secuencia está limitada por encima. Mientras que si an >= M, para todos los valores de n, entonces tal secuencia está limitada por debajo.

También es posible añadir prefijos al nombre de la secuencia basados en los elementos de la secuencia. Si todos los elementos de la secuencia son números enteros, entonces la llamamos secuencia de números enteros. Mientras que si todos los elementos de la secuencia son polinomios la llamamos una secuencia de polinomios y así sucesivamente.

También existen dos vías de secuencias infinitas o secuencia infinita-bi, la cual es una función del conjunto de todos los enteros en otro conjunto.

Supongamos una función f: {1, 2, 3, 4…} {1, 2, 3, 4…} define una secuencia A donde cada ai = f(i). Tal secuencia se denominaría multiplicativa cuando,

f(xy) = f(x) f(y), para todos los valores de x e y, donde x e y son co-primos.

Una serie es la sumatoria de la suma de todos los elementos de una secuencia. La suma de todos los elementos de una secuencia infinita se denomina serie infinita.

Que también puede ser denotado por,

2.10 Función implícita

Una función y (x) se llama implícita cuando está definida de la forma F (x, y) = 0 en lugar de la habitual.

Por ejemplo, puede probarse que la siguiente ecuación define una función implícita en cierta región de  entre las variables x e y:  

Diferenciación

Para poder derivar una función implícita se usa la Regla de la cadena, en el caso de la variable independiente no hay problema ya que se deriva directamente, para la variable dependiente se considera como una función que a su vez esta en función de la variable independiente:

Dada una función F(X,Y), implícita, si queremos calcular la derivada de y respecto de x: dy/dx=f´(X)

Si consideramos Y = F(x) es una función en términos de la variable independiente x y  G(y) es una función en términos de la variable dependiente y, dado que Y= f(x) , entonces para obtener la derivada: