Unidad 1

Unidad 1

1.1 La recta numérica.

1.2 Los números Reales.

1.3 Propiedades de los números reales.

1.4 Intervalos y su representación mediante desigualdades.

1.5 Resolución de desigualdades de primer grado con una incógnita y de desigualdades cuadráticas con una incógnita.

1.6 Valor absoluto y sus propiedades.

1.7 Resolución de desigualdades que incluyan valor absoluto.

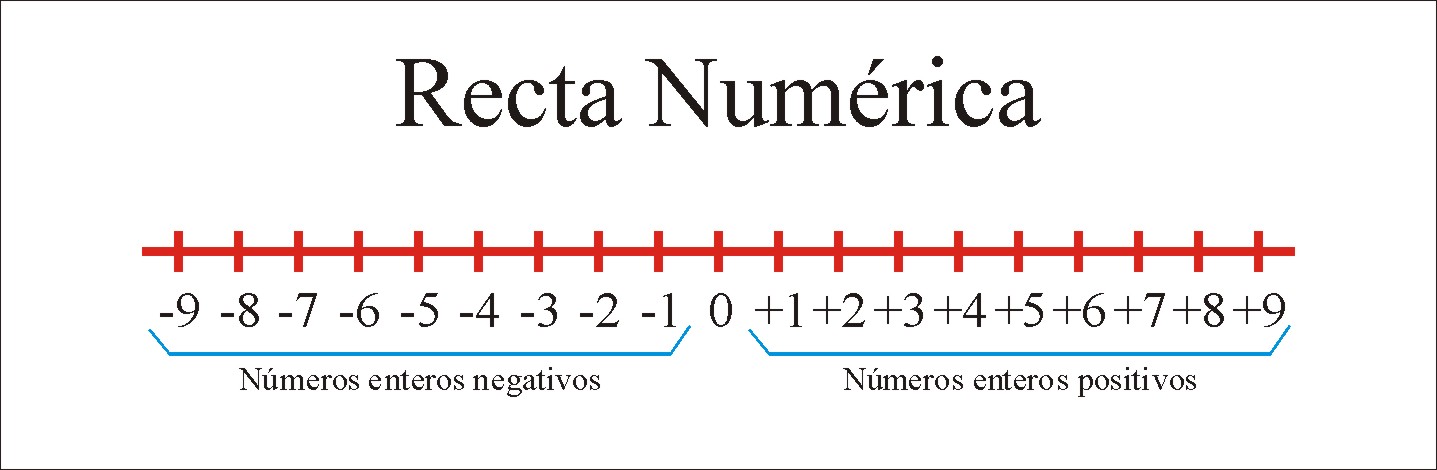
1.1 LA RECTA NUMÉRICA

Es una línea de una sola dimensión que está compuesta por una sucesión infinita de puntos, prolongada en una misma dirección. Numérico, por su parte, es un adjetivo que se refiere a lo que está vinculado a los números (los signos que expresan una cantidad)

1.2 Números Reales

Número real, cualquier número racional o irracional. Los números reales pueden expresarse en forma decimal mediante un número entero, un decimal exacto, un decimal periódico o un decimal con infinitas cifras no periódicas.

El conjunto de los números reales:

Número Naturales (N): números con los que contamos (también se les llama enteros positivos).

Enteros (E): conjunto de todos los números naturales con sus opuestos (negativos) y el cero. 

Racionales: conjunto formado por todos los números que se pueden escribir en la forma, donde m y n son enteros .

Número Reales (R): todos los racionales y los irracionales. Los números racionales tienen representaciones decimales repetitivas (periódicas), en tanto que los irracionales tienen representaciones no repetitivas infinitas.

                        1.3 PROPIEDADES DE LOS NÚMEROS REALES

Las propiedades que existen en los numeros rales son indispensables tanto por la ordenación de los numero, como tambien para poder hacer soluciones a los problemas matematicos que se nos pueda dificultar.

asi tambien los podemos observar y comprender mejor, como obtener soluciones y como es su representacion.

Propiedad Conmutativa de la Suma:

Establece que el orden en el que dos números reales se suman no afecta a su sumatoria.

Ejemplo: 3 + 7 = 7 + 3 = 10.

Propiedad Conmutativa de la Multiplicación:

De acuerdo con esta, cuando dos números reales se multiplican en diferentes órdenes, el resultado es siempre el mismo. En términos matemáticos,

Ejemplo: 4 X 3 = 3 X 4 = 12

Propiedad Asociativa de la Suma: Esta propiedad dice que la suma de tres números reales dados, manteniendo su orden, agrupa dos de ellos, y luego se añade el tercer número a la sumatoria del grupo. Matemáticamente,

Ejemplo: (2 + 3) + 4 = 2 + (3 + 4) = 9

Propiedad Asociativa de la Multiplicación: El producto de dos números reales se puede calcular de dos formas: De la primera forma, preservando el orden y multiplicando el número del producto del primer y segundo número al tercer número. La segunda forma de hacerlo es preservando el mismo orden y multiplicando el primer número con el producto del segundo y tercer número. El resultado en ambos casos será el mismo. Para ser específicos,

Ejemplo: (2 X 3) X 4 = 2 X (3 X 4) = 24

Propiedad de Identidad de la Suma: ‘0’es el número neutral, es decir, la identidad para la suma. La suma de cualquier número con 0 dará como resultado el propio número. Expresamente,

Ejemplo: 9 + 0 = 9

Propiedad de Identidad de la Multiplicación: Según esta propiedad de los Números Reales, el producto de cualquier número real con el elemento de identidad ‘1’ es el número real mismo.

Ejemplo: 6 X 1 = 6

Inverso aditivo: Para cada Número Real, existe su inverso, de tal manera que la suma del número con su inverso dará como resultado 0,

Ejemplo: 3 + (−3) = 0

Inverso multiplicativo: De acuerdo con este, para todo Número Real distinto de cero, existe otro número real tal que el producto de los dos es 1. Matemáticamente,

Ejemplo: 3 X 1/3 = 1

Ley distributiva: En los Números Reales, la multiplicación se puede distribuir sobre la suma y viceversa.

Ejemplo: 2 X (3 + 5) = (2 X 3) + (2 X 5) = 16

1.4 INTERVALOS Y SU PRESENTACIÓN MEDIANTE DESIGUALDADES

Las desigualdades es una forma: 10+3>6, que la podemos transformar en una inecuacion que cuando se introduce una incógnita (x): 10+x>6.

En la recta numérica existe una inecuacion de orden y que se puede dar en 3 alternativas: a>b,  a-=b y a<b.

intervalos cerrados

Son aquellos intervalos que incluyen los valores extremos a y b. Esto se expresa con la desigualdad  a ≤ x ≤ b, que significa que a es menor o igual que x y que x es menor o igual que b.

Otra manera de expresar intervalos cerrados es utilizando corchetes: [a , b]

intervalos abiertos

Son aquellos intervalos que excluyen los valores extremos a y b. Esto se expresa con la desigualdad  a < x < b, que significa que a es menor que x y que x es menor que b.

Otra manera de expresar intervalos abiertos es utilizando parentesis: (a , b)

Intervalos semi-abiertos

Son aquellos intervalos que solo incluyen a uno de sus extremos.

Existen dos casos: Abiertos por la izquierda que se representan con la desigualdad  a < x ≤ ∞, que significa que a es menor que x y que x es menor o igual que b.

También se puede expresar así: (a , b]

Intervalos infinitos

Son aquellos intervalos contienen una cantidad infinita de valores y que pueden o no tener un extremo en uno de sus lados. Infinito por ambos lados que se representan con la desigualdad  -∞ < x < ∞, que significa que -∞ es menor que x y que x es menor que ∞ 

 1.5 resolucion de desigualdades de primer grado con una       incognita y de desigualdades cuadraticas con una incognita

Las desigualdades de primer grado (lineales), se pueden resolver de una manera similar que las ecuaciones lineales.

Es decir, se puede despejar la incógnita utilizando operaciones idénticas en ambos lados de la desigualdad.

Como veremos en los ejemplos, es necesario tomar en cuenta una diferencia muy importante, pues cuando se multiplica una desigualdad por algún valor negativo, la dirección de la desigualdad se invierte, es decir, de menor que cambia a menor que y viceversa.

las desigualdades de segundo grado de acuerdo a las características de la expresión cuadrática, podemos determinar si la resolveremos por fórmula general, por factorización, ó despejando.

Además de tener en cuenta el efecto de la multiplicación por números negativos en la dirección de la desigualdad, también tenemos que considerar el efecto de la raiz cuadrada.

 .

1.6 VALOR ABSOLUTO

El valor absoluto o numérico de un número es la distancia del mismo con respecto al 0 en la recta numérica.

El valor absoluto de cualquier número es siempre positivo.

Para cualquier número, si:

 Entonces | x | = x  y  si

x ‹ 0 entonces | x | = -x

Las propiedades fundamentales del valor absoluto son:

No Negatividad: Establece que el valor absoluto de un número nunca puede ser negativo.

Definición Positiva: De acuerdo a esta simple propiedad, si el valor del módulo de un número real x es 0, entonces el valor absoluto de x es 0 y vice-versa.

| x | = 0 x = 0

Propiedad Multiplicativa: Esta significa que el módulo de un producto de dos números es siempre igual al producto de los módulos de ambos números tomados por separado.

| xy| = | x | | y |

Propiedad Aditiva: En concordancia con la propiedad multiplicativa, establece que el módulo del valor de la suma de dos números es siempre igual a la suma por separado del módulo de ambos números.

| x + y| = | x | + | y |

En combinación con estas cuatro propiedades fundamentales, algunas otras de las propiedades más importantes son:

Simetría: Establece que la definición básica del valor absoluto es, en otras palabras, ignorar el signo negativo.

| - x | = x

1.7 RESOLUCIÓN DE DESIGUALDADES QUE INCLUYAN VALOR ABSOLUTO

Patron 1: Menor desigualdad absoluta

De acuerdo con este patrón, si la desigualdad a ser resuelta es de la forma | s | <a, entonces en ese caso, la solución correspondiente siempre tendrá la forma de -a <s <a.

Este concepto es válido incluso para las desigualdades de alta complejidad.

Por ejemplo: | x + 3 | <7

De acuerdo con el patrón, puede ser reformulada como

= - 7 <x + 3 <+7

Después de replanteada siguiendo el patrón 1, ahora puede ser resuelta de acuerdo con los fundamentos de la desigualdad, es decir,

- 7 – 3 < x < + 7 – 3 - 10 < x < +4

Por tanto, la solución está en el intervalo de (−10, +4).

Patrón 2: Mayor desigualdad absoluta

De acuerdo con este patrón, si | s |› a es el patrón de la desigualdad dada, entonces la solución puede ser obtenida mediante separar la desigualdad en dos partes, que son s < –a o s > a .

Por ejemplo:| x + 5 | › 8

Siguiendo de acuerdo con el patrón x + 5 < - 8 o x + 5 > 8

Ahora, la desigualdad puede ser resuelta junta como

x < - 8 – 5 o x > 8 - 5

x < −13 o x < 3

Por tanto, la solución consiste en dos intervalos x < - 13 o x < 3.

Otra variedad de problemas pueden ocurrir cuando se da un par de desigualdades con el fin de encontrar las desigualdades con valor absoluto correspondiente. Para resolver este tipo de problemas, es necesario seguir algunos pasos. En primer lugar, mirando los extremos de las desigualdades dadas. El siguiente paso consiste en calcular la diferencia entre los extremos determinados. Ahora, ajustando las desigualdades con la mitad de la diferencia calculada dará las desigualdades en la forma que cualquiera de los dos patrones puede ser aplicado.

La aplicación de estas reglas puede ser demostrada con la ayuda de un ejemplo:

Supongamos que las desigualdades provistas son:

De acuerdo con las reglas, los extremos determinados son 24 y 19. Estos extremos están a 5 unidades de distancia. Por tanto, las desigualdades se puede ajustar entre la mitad de la diferencia, es decir −2.5 a +2.5.

Ahora, desde 19 – (−2.5) = 21.5 y 24 – 2.5 = 21.5, por tanto 21.5 se necesita para ser restado de todos los lados de las desigualdades.

x < 19 o x > 24

x – 21.5 < 19 – 21.5 o x – 21.5 > 24 – 21.5

x – 21.5 < –2.5 o x – 21.5 > 2.5

Se puede observar que el resultado es de la forma “mayor que”. Por tanto, el resultante de la desigualdad con valor absoluto es | x - 21.5 |› 2.5