Aplicaciones de la derivada
5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales
5.2 Teorema de Rolle, teorema de Lagrange o teorema del valor medio del cálculo diferencial.
5.3 Función creciente y decreciente. Máximos y mínimos de una función. Criterio de la primera derivada para máximos y mínimos. Concavidades y puntos de inflexión. Criterio de la segunda derivada para máximos y mínimos.
5.4 Análisis de la variación de funciones.
5.5 Cálculo de aproximaciones usando la diferencial.
5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales
PENDIENTE DE LA TANGENTE A LA CURVA:
Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma pendiente que la curva en ese punto.
Es igual al valor de la derivada en cualquier punto.Se representa matemáticamente:
PENDIENTE DE LA NORMAL A LA CURVA:
Una normal a una curva es una recta que es perpendicular a la tangente de la curva. La tangente y la normal en un mismo punto en cualquier superficie siempre son perpendiculares entre sí.
Es igual a la reciproca de la pendiente de la tangente a la curva. Se representa matemáticamente:
Una recta tangente a una curva en un punto, es una recta que al pasar por dicho punto y que en dicho punto tiene la misma pendiente de la curva. La recta tangente es un caso particular de espacio tangente a una variedad diferenciable de dimensión.
Sea  una curva, y
una curva, y  un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en
un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en  la curva no cambia repentinamente de dirección. La tangente a
la curva no cambia repentinamente de dirección. La tangente a  en
en  es la recta
es la recta  que pasa por
que pasa por  y que tiene la misma dirección que
y que tiene la misma dirección que  alrededor de
alrededor de  .
.
 una curva, y
una curva, y  un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en
un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en  la curva no cambia repentinamente de dirección. La tangente a
la curva no cambia repentinamente de dirección. La tangente a  en
en  es la recta
es la recta  que pasa por
que pasa por  y que tiene la misma dirección que
y que tiene la misma dirección que  alrededor de
alrededor de  .
.
La tangente es la posición límite de la recta secante (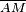 ) (el segmento
) (el segmento 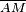 se llama cuerda de la curva), cuando
se llama cuerda de la curva), cuando  es un punto de
es un punto de  que se aproxima indefinidamente al punto
que se aproxima indefinidamente al punto  (
( se desplaza sucesivamente por
se desplaza sucesivamente por 
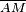 ) (el segmento
) (el segmento 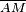 se llama cuerda de la curva), cuando
se llama cuerda de la curva), cuando  es un punto de
es un punto de  que se aproxima indefinidamente al punto
que se aproxima indefinidamente al punto  (
( se desplaza sucesivamente por
se desplaza sucesivamente por 
Si  representa una función f (no es el caso en el gráfico precedente), entonces la recta
representa una función f (no es el caso en el gráfico precedente), entonces la recta 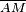 tendrá como coeficiente director (o pendiente):
tendrá como coeficiente director (o pendiente):
 representa una función f (no es el caso en el gráfico precedente), entonces la recta
representa una función f (no es el caso en el gráfico precedente), entonces la recta 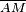 tendrá como coeficiente director (o pendiente):
tendrá como coeficiente director (o pendiente):
Donde 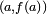 son las coordenadas del punto
son las coordenadas del punto  y
y 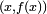 las del punto
las del punto  . Por lo tanto, la pendiente de la tangente TAserá:
. Por lo tanto, la pendiente de la tangente TAserá:
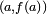 son las coordenadas del punto
son las coordenadas del punto  y
y 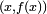 las del punto
las del punto  . Por lo tanto, la pendiente de la tangente TAserá:
. Por lo tanto, la pendiente de la tangente TAserá:
Es, por definición, f '(a), la derivada de f en a.
La ecuación de la tangente es  :
:
 :
:
La recta ortogonal a la tangente  que pasa por el punto
que pasa por el punto 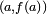 se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por
se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por  . Siendo su ecuación:
. Siendo su ecuación:
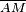 que pasa por el punto
que pasa por el punto 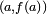 se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por
se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por  . Siendo su ecuación:
. Siendo su ecuación:
suponiendo claro está que 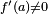 . Si
. Si 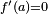 entonces la recta normal es simplemente
entonces la recta normal es simplemente  . Esta recta no interviene en el.
. Esta recta no interviene en el.
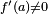 . Si
. Si 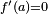 entonces la recta normal es simplemente
entonces la recta normal es simplemente  . Esta recta no interviene en el.
. Esta recta no interviene en el.
5.2 Teorema de Rolle, teorema de Lagrange o teorema del valor medio del cálculo diferencial.
Teorema de Rolle
Michael Rolle (1652-1719)
Si una función es continua en un intervalo cerrado [a,b], derivable en el intervalo abierto (a,b) y f(a)=f(b), entonces existe al menos un punto c entre a y b para el cual f'(c)=0.
H) f es continua en [a,b]
f es derivable en (a,b)
f(a)=f(b)
T) Existe c perteneciente a (a,b) / f'(c)=0
H) f es continua en [a,b]
f es derivable en (a,b)
f(a)=f(b)
T) Existe c perteneciente a (a,b) / f'(c)=0
Interpretado geométricamente, significa que si una curva alcanza el mismo valor en dos puntos, entonces debe poseer una tangente horizontal en algún punto intermedio.
Demostración:
f es continua en [a,b] => por teo. de Weierstrass f tiene máximo absoluto M y mínimo absoluto m en [a,b].
Para todo x perteneciente a [a,b] m <= f(x) <= M.
Existe x1 perteneciente a [a,b] / f(x1)=M.
Existe x2 perteneciente a [a,b] / f(x2)=m.
Si m = M => para todo x perteneciente a [a,b] f(x) = M => f'(x) = 0
Sino, m < M => por lo menos uno de los puntos, x1 o x2, corresponde al interior del intervalo, a (a,b), por ejemplo x2.
=> (a,b) se comporta como un entorno de x2.
Se cumple que para todo x perteneciente a (a,b) f(x2) <= f(x)
=> Por def. de mínimo relativo f presenta un mínimo relativo en x2. (1)
f es derivable por hipótesis. (2)
De 1) y 2), por Condición necesaria para la existencia de extremos relativos f'(x2)=0
Teorema de Lagrange o del valor medio
Joseph Louis Lagrange (1736 - 1813)
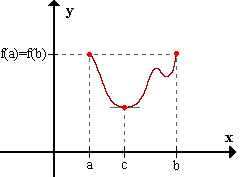
Si f(x) es continua en el intervalo cerrado [a,b] y derivable en todo punto del intervalo abierto (a,b), entonces existe al menos un punto c donde f'(c) = (f(b) - f(a))/(b - a).
H) f(x) es continua en [a,b]
f(x) es derivable en (a,b)
T) Existe c perteneciente a (a,b) /f'(c)=(f(b) - f(a))/(b - a)
H) f(x) es continua en [a,b]
f(x) es derivable en (a,b)
T) Existe c perteneciente a (a,b) /
Geométricamente, (f(b) - f(a))/(b - a) es la tangente del ángulo que forma la secante que pasa por los puntos A(a,f(a)) y B(b,f(b)) de la curva, con el eje ox.
f'(c) es la tangente del ángulo que forma la recta tangente a la curva en el punto c, con el eje ox.
f'(c) es la tangente del ángulo que forma la recta tangente a la curva en el punto c, con el eje ox.
Entonces, el teorema expresa que existe al menos un punto en el intervalo (a,b) donde la tangente a la curva es paralela a la recta que pasa por A y B.
Demostración:
Definamos una función auxiliar g(x) = f(x) + hx, h perteneciente a R.
g es continua en [a,b] por ser suma de funciones continuas.
g es derivable en (a,b) por ser suma de funciones derivables.
Queremos que g(a) sea igual a g(b) para aplicar el teorema de Rolle
g es derivable en (a,b) por ser suma de funciones derivables.
Queremos que g(a) sea igual a g(b) para aplicar el teorema de Rolle
=> f(a) + ha = f(b) + hb => f(a) - f(b) = hb - ha =
f(a) - f(b)
=> h = -----------
b - a
=> por teo. de Rolle, existe c perteneciente a (a,b) / g'(c) = 0
g'(x) = f'(x) + h
f(b) - f(a)
g'(c) = f'(c) + h = 0 => f'(c) = -----------
b - a
Considérese por ejemplo, el caso donde x es el tiempo y f(x) la distancia de un automóvil desde su punto de partida a lo largo de cierto camino.
Entonces (f(b) - f(a))/(b - a) es la velocidad promedio del automóvil en el período b - a. (Recordar que velocidad = distancia/tiempo)
Por lo tanto f'(a)=limx->a (f(x) - f(a))/(x - a) es la velocidad del auto en el tiempo a.
Si por ejemplo el auto ha recorrido 200km. en 2 hs., la velocidad promedio fue de 100km. por hora.
Por el teorema de Lagrange podemos decir que, al menos en un momento durante esas dos horas, el auto tuvo una velocidad de exactamente 100km/h.
Entonces (f(b) - f(a))/(b - a) es la velocidad promedio del automóvil en el período b - a. (Recordar que velocidad = distancia/tiempo)
Por lo tanto f'(a)=limx->a (f(x) - f(a))/(x - a) es la velocidad del auto en el tiempo a.
Si por ejemplo el auto ha recorrido 200km. en 2 hs., la velocidad promedio fue de 100km. por hora.
Por el teorema de Lagrange podemos decir que, al menos en un momento durante esas dos horas, el auto tuvo una velocidad de exactamente 100km/h.
5.3 Función creciente y decreciente. Máximos y mínimos de una función. Criterio de la primera derivada para máximos y mínimos. Concavidades y puntos de inflexión. Criterio de la segunda derivada para máximos y mínimos.
Funciones Creciente y Decreciente.
Definición:
Si al aumentar el valor de x el valor de su imagen ((x) también se incrementa, se dice que lagráfica de la función crece y, por el contrario, cuando el valor x aumenta disminuye ((x), decimos que la función decrece.
Simbólicamente podríamos definir:
(es creciente en un intervalo [a, b] ((x1 (x2 ([a, b]: x1 ( x 2 ((x1) ( ((x2)
(es decreciente en un intervalo [a, b] ( (x1 (x2 ([a, b]: x1( x 2 ((x1) ( ((x2)
Definición:
Si al aumentar el valor de x el valor de su imagen ((x) también se incrementa, se dice que lagráfica de la función crece y, por el contrario, cuando el valor x aumenta disminuye ((x), decimos que la función decrece.
Simbólicamente podríamos definir:
(es creciente en un intervalo [a, b] ((x1 (x2 ([a, b]: x1 ( x 2 ((x1) ( ((x2)
(es decreciente en un intervalo [a, b] ( (x1 (x2 ([a, b]: x1( x 2 ((x1) ( ((x2)
Se dice que una función tiene un valor máximo en el punto v, cuando el valor de f(v) es mayor que el valor en cualquiera de los puntos vecinos.
Del mismo modo, cuando el valor es menor que el valor en sus puntos vecinos, entonces ese valor se convierte en el valor mínimo de la función.

Criterios de la derivada de primer orden para máximos y mínimos:
Los relativos máximos o mínimos de la función pueden ser encontrados mediante la búsqueda de la primera derivada de la función.
Si la primera derivada resulta ser mayor que 1, en ese caso, se dice que la función está creciendo sobre el intervalo.
En el caso inverso, cuando la primera derivada resulta ser menor que 1, entonces se dice la que función es decreciente en ese intervalo.
Concavidades y puntos de inflexión:
El concepto de concavidad se utiliza para determinar si la gráfica de la función es de la forma cóncava hacia arriba o cóncava hacia abajo.
Si para los valores dados de intervalo, la doble derivada de la función es mayor o igual que 0, entonces el gráfico de la función será cóncavo hacia arriba, y cuando la doble derivada se convierte en menor que 0, entonces la forma de la gráfica será cóncava hacia abajo.

Ahí se encuentra una posición en la cual el gráfico de la función cambia su forma de cóncava hacia abajo a cóncava hacia arriba o vice-versa.
Estas posiciones, o más bien los puntos, son conocidos como puntos de inflexión.
En estos puntos de inflexión, la doble derivada de la función se convierte en 0.
Criterios de la derivada de segundo orden para máximos y mínimos:
La segunda derivada también puede ser utilizada con el fin de encontrar el punto máximo o mínimo de la función.
1). Se dice que una función posee el máximo local en un punto específico, si, la doble derivada de la función en ese punto es menor que 0.
2). Se dice que una función posee mínimo local en un punto específico, si, la doble derivada de la función en ese punto es mayor que 0.
3). Cuando la doble derivada resulta ser 0, en ese caso, es posible que el punto sea un punto de inflexión.
5.4 Análisis de la variación de funciones.
Cuando la variación total de cualquier función particular es finita, en ese caso, esa función se conoce como Función de Variación Acotada, que puede ser abreviada como función BV (Bounded Variation por sus siglas en inglés). El gráfico correspondiente de la función BV se dice entonces que se comporta bien en un sentido preciso. La función BV tiene amplias aplicaciones en el campo de las matemáticas, y es utilizada en algunos de los teoremas más importantes, tal como son los Teoremas de Fourier. En el caso de la funciones continuas que contienen sólo una variable, la variación acotada implica la distancia finita cubierta por un punto a lo largo del eje y. Otra clasificación establece que las funciones de variación acotada, tienen la propiedad de intervalo cerrado, son las funciones que se pueden establecer como la diferencia entre dos monótonas acotadas.
La variación Acotada de una función determinada en el intervalo [x, y] puede ser establecida como:
Donde S es el conjunto acotado:
La variación resulta ser infinita si el conjunto no es acotado. El supremo de S puede ser llamado también como Variación Total o sólo la variación de f y se denota como V (f; x, y) o simplemente V (x). Existen ciertos teoremas que pueden ser útiles para el análisis de la variación de la función:
1). Si en el conjunto [x, y], la función está incrementando, en ese caso, es la función de variación acotada en el conjunto [x, y] y consecuentemente V [g [x, y]] = g(y) – g(x).
2). Si en el conjunto [x, y] la función es constante, entonces es la función de variación acotada en el conjunto [x, y] y entonces V [g [x, y]] = 0.
Por ejemplo, la función g(r) = c es una función de variación acotada constante en el intervalo [x, y].
| g (ri) – g (ri - 1)| = 0 por cada partición del conjunto [a, b]. Por tanto, V (g, [x, y]) = 0.
3) En el conjunto [x, y] si, g y f son las funciones de variación acotada y c es constante, en ese caso
a). g es una función de variación acotada en el intervalo [x, y].
b). g es una función de variación acotada en cada subintervalo cerrado del intervalo [x, y].
c). cg es también una función BV en el conjunto [x, y].
d). g + f y g –f son BV en el conjunto [x, y]
e). gf es también BV en el conjunto [x, y].
Algunos datos más útiles acerca de estas funciones especiales se pueden establecer como que una función de variación acotada se puede expresar también por la divergencia de 2 funciones crecientes.
Del mismo modo, todas las funciones totalmente continuas son de naturaleza BV, sin embargo, no es necesario que todas las funciones continuas BV deban ser totalmente continuas.
La función f puede ser considerada como BV en el conjunto [x, y] si, la derivada de f se encuentra acotada en [x, y].
Además, cuando dos funciones variación acotada se multiplican entre sí, entonces la resultante es también una función de variación acotada.
Hay algunas propiedades básicas que son seguidas por las Funciones de Variación Acotada:
1) Las Funciones de Variación Acotada pueden tener discontinuidad de primer tipo, es decir, discontinuidad de salto.
5.5 Cálculo de aproximaciones usando la diferencial.
Se define en esta sección el concepto de la diferencial, que nos permite representar la derivada como un cociente y hallar el valor aproximado de la variación de una función alrededor de un punto.
La definición esta motivada por el siguiente razonamiento geométrico. Sea P(x0, y0) un punto fijo sobre la gráfica de y = f (x) Tomando el punto P(x0, y0) como origen, se introduce un nuevo sistema de coordenadas cuyos ejes dx y dyson paralelos a los ejes antiguos.
En este nuevo sistema de coordenadas, la recta tangente en el punto P pasa por el origen y en consecuencia, su ecuacion es bastante simple, a saber: dy = mdx, donde m es la pendiente. Ahora, como la pendiente en el nuevo sistema es la misma que la del antiguo, esto es m = f ¡¯(x), se tiene entonces: dy = f ¡¯(x) dx Lo anterior nos permite dar la definición formal de las diferencial.
La definición esta motivada por el siguiente razonamiento geométrico. Sea P(x0, y0) un punto fijo sobre la gráfica de y = f (x) Tomando el punto P(x0, y0) como origen, se introduce un nuevo sistema de coordenadas cuyos ejes dx y dyson paralelos a los ejes antiguos.
En este nuevo sistema de coordenadas, la recta tangente en el punto P pasa por el origen y en consecuencia, su ecuacion es bastante simple, a saber: dy = mdx, donde m es la pendiente. Ahora, como la pendiente en el nuevo sistema es la misma que la del antiguo, esto es m = f ¡¯(x), se tiene entonces: dy = f ¡¯(x) dx Lo anterior nos permite dar la definición formal de las diferencial.
En cálculo, la diferencial representa la parte principal del cambio en una función y = ƒ(x) con respecto a los cambios en la variable independiente. La misma diferencia se define por una expresión de la forma
dy = {dy}{dx}\dx
como si el derivados dy/dx representa el cociente de una cantidad dy por una cantidad dx. También se escribe
df(x) = f’(x)dx.
El significado preciso de tales expresiones depende del contexto de la aplicación y el nivel requerido de rigor matemático. En los tratamientos modernos matemáticos rigurosos, las cantidades dy y dx son simplemente más real variables que puede ser manipulado como tal. El dominio de estas variables pueden tener un significado geométrico particular, si el diferencial se considera un particular forma diferencial, o la importancia de análisis, si el diferencial se considera como una aproximación lineal al incremento de una función. En las aplicaciones físicas, las variables dx y dy a menudo, deben ser muy pequeñas (“infinitesimal”).
El diferencial fue introducido por primera vez a través de definiciones intuitivas o heurístico Gottfried Wilhelm Leibniz, que pensaba de la diferencia dy como lo infinitamente pequeño (o infinitesimal) cambio en el valor y de la función, que corresponde a un cambio infinitamente pequeño dx en el argumento de la función x. Por esa razón, la razón instantánea de cambio de y con respecto a x, que es el valor de la derivados de la función, se denota por la fracción
{dy}{dx}
en lo que se llama el Leibniz notación para los derivados. El cociente dy/dx es, por supuesto, no lo infinitamente pequeño, sino que es un número real.
El uso de los infinitesimales en esta forma fue muy criticado, por ejemplo, el famoso panfleto “El Analista” por el obispo Berkeley. Augustin-Louis Cauchy (1823) se define la diferencia, sin apelar a la teoría atómica de los infinitesimales de Leibniz. En cambio, Cauchy, tras D’Alembert, se invierte el orden lógico de Leibniz y sus sucesores: el derivado de sí mismo se convirtió en el objeto fundamental, que se define como un límite de los cocientes de diferencia, y los diferenciales se definieron a continuación, en términos de la misma. Es decir, uno era libre de definir el diferencial dy por una expresión
dy = f’(x)dx
5.6 Problemas de optimización y de tasas relacionadas.
La optimización se refiere al tipo de problema que se ocupa de la determinación de la forma más apropiada para realizar cierta tarea. Con el fin de resolver estos problemas, se calculan los valores mínimos y máximos de la función. Estos incluyen encontrar la distancia mínima para llegar a un punto, el costo mínimo para hacer determinada operación, etc. La función cuyo máximo o mínimo necesita determinase por lo general está sujeta a ciertas restricciones que deben tomarse en cuenta.
Estos problemas son diferentes a los problemas utilizados para encontrar los valores mínimos o máximos locales. Los Problemas de optimización sólo se ocupan de los valores máximos o mínimos que una función puede tomar y no del mínimo o máximo en un intervalo. Es decir, la optimización busca el mínimo o máximo global (absoluto) y no el local. El mínimo o máximo absoluto es el mayor entre el mínimo o máximo local, respectivamente.
Puede haber casos, donde el mínimo o máximo global no existe para una función. En estos el dibujo de la gráfica para la función correspondiente puede ayudar en gran manera.
Hay algunos pasos que deben seguirse con el fin de desglosar un problema de optimización:
1). Lo primero y más importante es identificar las variables y constantes de la función. Esto ayuda a determinar la parte de la función que será minimizada o maximizada.
2). Escribir la fórmula adecuada para la función particular, para lo cual tenemos que calcular el mínimo o máximo.
3). Ahora, la fórmula será escrita en términos de una sola variable, es decir, f®.
4). Establezca la diferenciación de f® a 0, f ‘® = 0, y resuelva a través de observar todas las limitaciones y otros valores críticos para encontrar los valores extremos.
Por ejemplo, considere la función, g ® = -r2 + 4r – 2. Y siendo el intervalo en el cual el valor máximo será encontrado [0, 1]. Calculando g ‘® se obtiene,
g’ ® = −2r + 4 = 0
Por lo tanto, 2 viene a ser un valor crítico, luego reemplazando el 2 en la función g (2) = 2. Ahora sustituyendo uno por uno los valores del intervalo en el lugar de r, obtenemos,
g (0) = −2 g (1) = 1
Se puede observar, que el valor máximo de g® en [0, 1] es 2.
Un tipo parecido de problema es el problema de las tasas relacionadas. Se trata de un problema en el que se proporciona la tasa de variación de al menos una variable de la función y en el problema se necesita buscar la otra tasa de variación.
También hay ciertas reglas simples para resolver estos problemas:
Considere que f(a) sea una función con dos variables a y b, las cuales cambian con el tiempo y la tasa de variación de a es dada con el tiempo, es decir,  .
.
 .
.
1). En primer lugar, encontrar la derivada de f(a), es decir, f ‘(a)
2). Ponga el valor de a en la ecuación
3).Entonces multiplíquelo con  para obtener
para obtener 
 para obtener
para obtener 
Aplicar las reglas en un ejemplo proporcionará una mejor comprensión:
Suponga que la pregunta dada dice lo siguiente: Se está bombeando aire a un globo esférico de 4 cm de radio a 5 cm3 / seg. Entonces, el ritmo de cambio del radio del globo necesita ser calculado.
Se puede observar que el radio y el volumen son las variables de las funciones correspondientes.  es dada y es igual a 5 cm3/seg y necesita encontrarse. Como
es dada y es igual a 5 cm3/seg y necesita encontrarse. Como  V= 4 r3 / 3. Diferenciando ambos lados, se obtiene
V= 4 r3 / 3. Diferenciando ambos lados, se obtiene  . Ahora sustituyendo el valor de en esta ecuación, se obtiene
. Ahora sustituyendo el valor de en esta ecuación, se obtiene 
 es dada y es igual a 5 cm3/seg y necesita encontrarse. Como
es dada y es igual a 5 cm3/seg y necesita encontrarse. Como  V= 4 r3 / 3. Diferenciando ambos lados, se obtiene
V= 4 r3 / 3. Diferenciando ambos lados, se obtiene  . Ahora sustituyendo el valor de en esta ecuación, se obtiene
. Ahora sustituyendo el valor de en esta ecuación, se obtiene 








